글쓴이 : SOONDORI
프랑스 수학자 Joseph Fourier(1768 ~ 1830)가 제안한 수학적 개념에 기초하여 어떤 주파수를 1) 시간(X축) 대 강도(Y축)로 표현하는 일반적인 표현방법에서 그 주파수를 2) 주파수 대역(X축) 대 강도(Y축)로 변환하여 표현하는 것을 ‘푸리에 변환(Fourier Transform)’이라고 한다. 오디오 세상뿐만 아니라 다양한 연구현장, 산업현장 등에서 응용되고 있다.
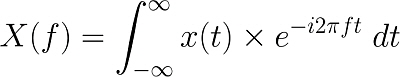
(t는 시간, f는 주파수, x(t)는 시간축으로 표현되는 값, X(f)는 주파수축으로 표현되는 값)
최초 대상 파형과 변환 파형 두 가지는 가역적으로 분해, 복원될 수 있고 논리상 신호의 훼손, 손상은 없으며 관찰자 관점만 달라진다. 레고-블럭으로 만든 물체가 있고 물체를 분해하여 부품 그대로 다른 형상으로 재조립하는 장면을 상상하면 되는 이 변환행위를 ‘도메인(Domain, 局面) 변환’이라고도 한다.
■ 왜 이런 것이 필요할까?
다소 관념적인 상황을 설정하고 정리를 해보자면… 현실 세상의 어떤 신호는 절대로 순수하지 않다.
예를 들어 완벽한 Sine 파형이 오실로스코프에서 관찰되었다고 할 때 그것은 사람이 그냥 그렇게 인지하는 것뿐이다. 만일 사인파의 특정 포인트를 무한대 배율을 가진 돋보기로 관찰한다면? 그 안에 다양한 잡신호나 노이즈, 정의되지 않은 주파수(신호)들이 포함되어 있음을 알 수 있다. 즉, 사람이 완벽하다고 인지하고 말하는 시그널-제너레이터의 신호 그것을 표현한 오실로스코프상의 싸인파조차 다양한 파형들의 복합 신호인 셈.
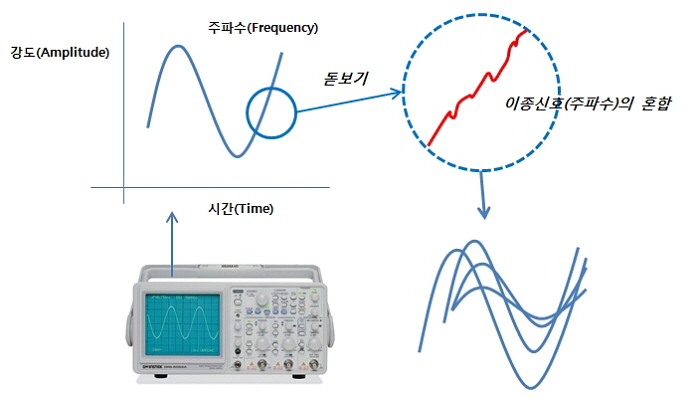
아래 그림의 좌측은 오실로스코프로 관측되는 통상적인 파형을, 우측은 퓨리에 변환의 결과물인 어떤 파형을 보여주고 있다.
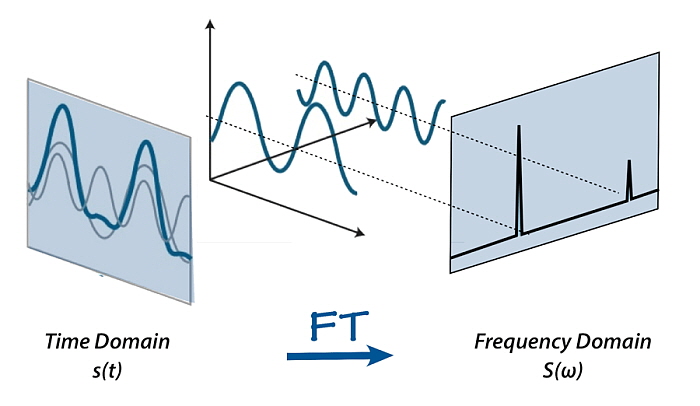
(출처 : http://mriquestions.com/uploads/3/4/5/7/34572113/3311485_orig.gif)
좌측은 크고 작은 두 가지 신호들이 조합된 복합파형이고 우측은 그 복합파형을 퓨리에변환으로 처리하여 두 원천 파형을 주파수 대역(X축)과 강도(Y축)로 분해/분리하여 재정리한 것이다.
좌측 화면으로는 그 안에 무엇이 포함되어 있는지를 알 수 없지만 우측 화면으로는 소속된 신호들의 특성을 일목요연하게 확인할 수 있다. 어떤 주파수들이 들어있는지와 각각의 강도가 분리 표현된다.
다시 정리하자면 푸리에 변환기(프로그램이나 하드웨어 장비)를 쓰면 복합신호에 포함된 여러가지 주파수(신호)들을 사람이 보고 이해하기 쉽다는 것. 여기서, 좌측은 시간을 주축(X축)으로 표현하고 있으므로 Time Domain이라 하고 우측은 주파수가 주축이므로 Frequency Domain이라고 한다.
이쯤에서 푸리에 변환을 ‘타임 도메인과 주파수 도메인을 가역적으로 전환시키는 수학적 방법론’ 정도로 이해해도 무방하겠다. 비유를 하자면 스마트-폰을 가로방향으로 볼 것이냐 아니면 기기를 돌려서 세로방향으로 볼 것이냐를 선택하는 정도? 물론 화면의 원천 콘텐츠(시간, 강도, 주파수)는 바뀌지 않았다.
[ 관련 글 ]
피타고라스와 音의 수학
스피커 진동과 클라드니 도형 그리고 에너지
■ 어떻게 변환을 하는가?
구현관점에서 푸리에 공식은 결국 ‘연산’이다.
예를 들어 변환공식을 프로그램으로 만들어 신호처리를 담당할 연산기 안에 집어 넣으면 된다. 다만, 원론적인 방법을 준수하고 방대한 샘플을 다루자면 큰 연산능력이 요구되므로 흔히 ‘고속 푸리에 변환(FFT; Fast Fourier Transform)’라는 간략화 기법(예: 쿨리-튜키 알고리즘, Cooley-Tukey algorithm)을 사용하고 한정된 샘플을 처리한다. 그리하여 연산성능이 다소 떨어지는 저가형 마이크로컨트롤러에서도 푸리에 변환기를 구현할 수 있다.
다음은 C-언어 고속 프리에 변환 샘플-소스인데 불과 ‘몇 줄 코딩으로 FFT 변환기 구현이 가능함’을 보여준다. 참고로 마이크로컨트롤러 소스를 코딩할 때는 부동소수점 연산이 지원되는 컴파일러를 사용해야 하고 하드웨어는 입력부 노이즈 등 외란요소의 개입을 최소화할 수 있도록 신경써야 한다.

(출처 : https://rosettacode.org/wiki/Fast_Fourier_transform)
■ 시각적 상상을 자극하는 장치들
이제 시각적 상상과 착안, 이해를 위하여 1) 주파수를 기준으로 파형을 볼 것인가, 2) 시간축을 기준으로 파형을 볼 것인가라는 두 가지 선택안을 여하히 처리해주는 도구(푸리에 변환기)들을 나열해 보면 다음과 같다.
모두 가로축(X축)은 주파수(Frequency 또는 구간을 지정한 Frequency Band), 세로축(Y축)은 강도(Amplitude)로 구성된 2차원 평면 지시계를 쓰고 있음에 주목한다.

(전문장비로서의 스펙트럼 애널라이저)
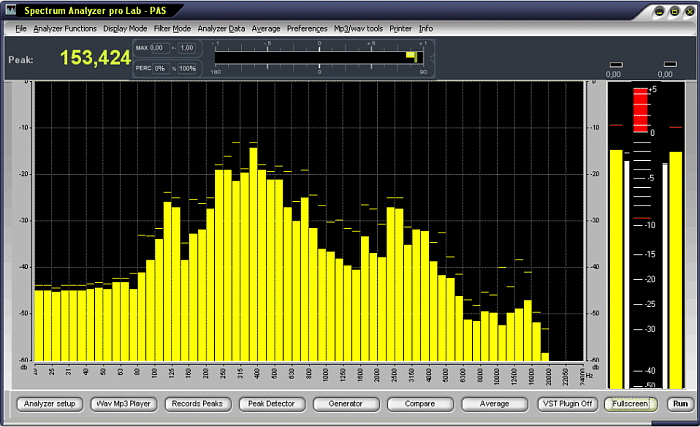
(프로그램으로 제작된 스펙트럼 애널라이저)

(Pioneer GR-777그래픽 이퀼라이저, FFT 연산기능을 내장한 전용 IC가 사용된 사례)

(출처 : http://www.kaleebo.com/uploads/9/4/9/7/9497775/9382543_orig.jpg)
다음은 연산기 IC를 쓰지 않고 수동소자 Band Pass Filter로 주파수 대역들을 분리한 후 다채널 LED 레벨미터에 연결한 것으로 추정되는 사례이다. 말인 즉, 스펙트럼이 제시된다고 해서 무조건 푸리에 변환기가 쓰였다고 볼 수는 없다는 것.

(출처 : https://i.ytimg.com/vi/gxREGgbmX6M/maxresdefault.jpg)
다음 글에서는 무한한 능력의 퓨리에 변환기를 갖고 있다 가정하고 특정한 입력, 출력 신호들이 어떻게 보이고 그것이 어떻게 해석되는 지를 정리해보기로 한다. 거론 키워드는 진공관 홀수/짝수 배음, 고조파(Harmonic, 高調波), 안테나 신호, 밴드 필터링 등.
* 관련 글 : 오디오의 주파수와 푸리에 변환 (2)





어쩌다 미적분 책을 다시 들여다보고 있는데, 푸리에 함수가 나와서 조금 놀랬습니다 아 이렇게 쓰이는 구나..
오실로스코프를 하나 장만했는데, 주파수 도메인으로 변환을 하면, 그 반응 속도가 느린데 원래 그런 건지요? 머랄까 실시간으로 음악에 맞춰서 그래프가 움직여야 할 것 같은데, 그 반응이 느려서 실제로는 이퀄라이저 느낌으로 체감이 안되는 것 같습니다.
유튭을 찾아보니,, 음악에 맟춰 실시간으로 그래프를 보여주는 것이 있는 것 같은데.. 어렵네요ㅜㅜ
안녕하세요? 동네 산책을 하고 왔는데 너무 조용한 주말입니다.
왜 느릴까요? 어떤 디지털 오실로스코프인지 모르겠습니다만…
내장형 또는 모듈 부착형 FFT가 간이 기능이기 때문에? 그리고 연산을 위한 기초 데이터 수집 그러니까 낮은 주파수에서 샘플링 변수가 심각하게 관여하기 때문에? 네… EQ에 달려 있는 오디오 스펙트럼 표시 장치처럼 빠르고 깔끔하고 예쁘게 동작하지는 않을 듯합니다. 혹시 모르니까 DSO 환경 설정을 확인해보시고요.
유튜브 동영상은 FFT가 아니라… 두 채널을 묶는 X-Y 연산 모드 그러니까 리사주 곡선(Lissajours Curve)을 만드는, 조금은 본질적인 오실로스코프의 기능을 사용하니까 아무렇게나 특히, 빠르게 처리되는 것이겠네요요.
여기서 X-Y 모드와 FFT 모드는 처리 논리가 다릅니다. X-Y는 CH1-CH2와 같이 정말로 아나로그적, 디지털적 실시간 빼기(또는 더하기)를 하는 것이고 FFT는 데이터를 획득하고 메모리에 적재한 다음에 FFT 논리에 따라 계산을 하지요. 아무래도 MCU 연산 파워와 시간이 더 필요할 것입니다. 그것 때문에라도 정식 스펙트럼 애널라이저가 오실로스코프보다 비싼 것이겠고요?!
—
제가 쓰는 TEK TDS-220은 TDS2MM이라는 모듈을 붙이면 X-Y 모드 하위 메뉴에 FFT를 쓸 수 있다고 합니다. 그런데 그게 없네요. TDS-2CM? 아무튼 GPIB/RS-232 포트 모듈만 달려 있습니다. 그게 있는 줄도 모르고 있었고요. 검색해보니 250불이라 하며… 차라리 SA를 하나 사는 게 낫겠습니다. 사용 빈도가 매우 낮아서 긴가민가하지만요.